Rebasing
The base period is an important point in time for a price index, as it gives the fixed reference point to which price changes are measured against. Having to choose a base period at all, however, introduces a potential problem: what works as a base period for one use of a price index may not work for another. Fortunately, the choice of base period doesn’t have much impact on the economic content of a price index—in most cases a new base period can be chosen for an index without needing to recompute the entire index series.
For a geometric index, the choice of base period has no impact on the economic content of a price index—the change in price between any two periods is the same regardless of the base period. The base period simply standardizes the index to a particular level. This can be seen by recalling that a geometric index can always be factored into two geometric indices. Given an index series with period 0 as the base period, the index value in period \(t\) with period \(k\) as the base period can always be found by simply dividing the index value in period \(t\) by the index value in period \(k\) \[\begin{align*} I^{G}(k, t) &= \prod_{i = 1}^{n} \left(\frac{p_{it}}{p_{ik}}\right)^{\omega_{i}} \\ &= \frac{\prod_{i = 1}^{n} \left(\frac{p_{it}}{p_{i0}}\right)^{\omega_{i}}}{\prod_{i = 1}^{n} \left(\frac{p_{ik}}{p_{i0}}\right)^{\omega_{i}}} \\ &= \frac{I^{G}(0, t)}{I^{G}(0, k)}. \end{align*}\]
Hence, dividing through the index series by the period \(k\) index value produces an index series that is the same as if period \(k\) were originally chosen as the base period. This is known as rebasing an index, and means that a change in price between two periods can be computed by simply scaling the price index. This also explains why the base period gets a value in the index series, for otherwise the index series would shrink each time the index is rebased.
The chart below gives an example of how rebasing changes the time series. The index with a base period of December is simply the index with a base period of January divided by the value of the index in December (105). This simply shifts the index with January as the base period down, and squashes it a little, but does not change the relative shape of the time series.
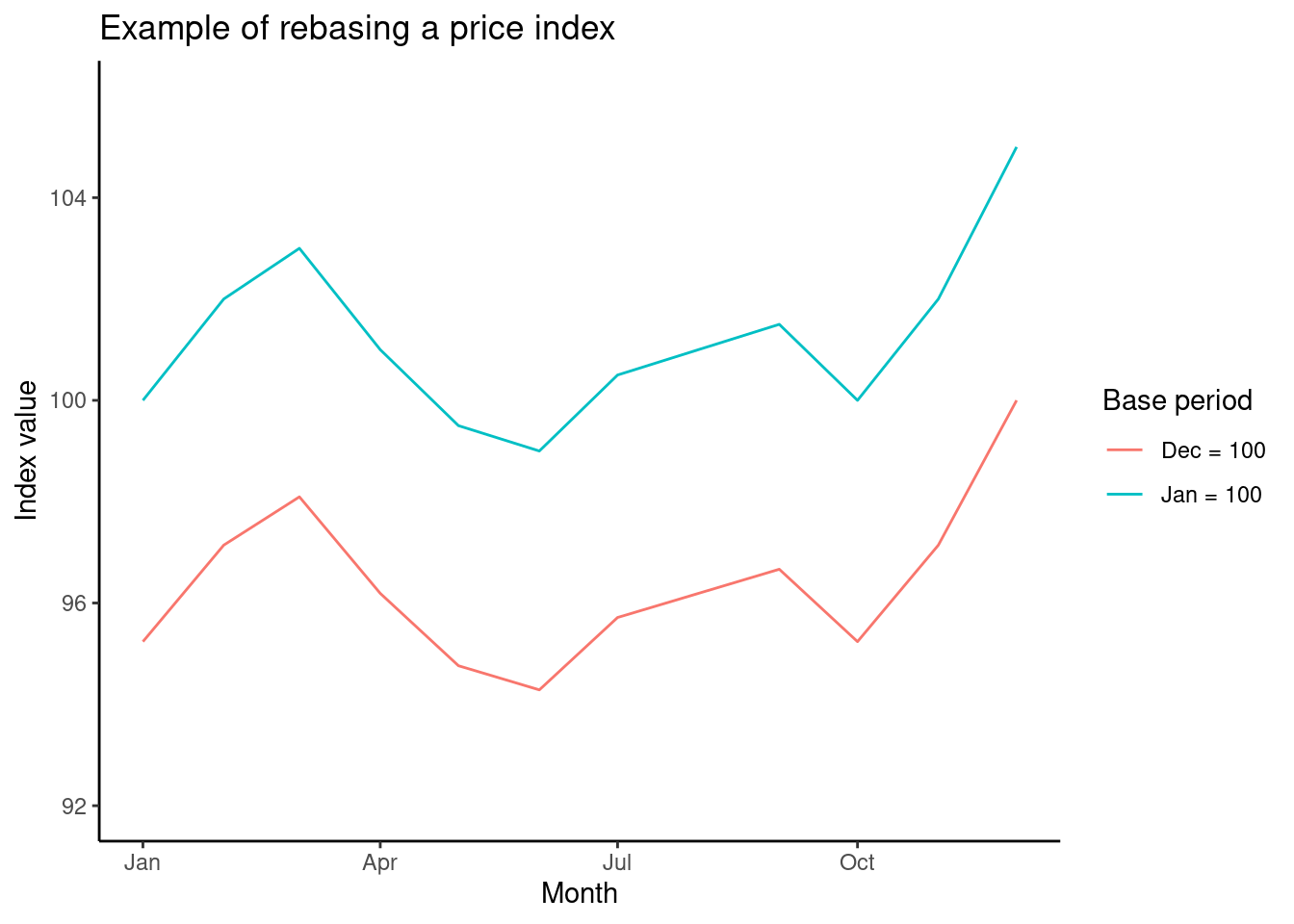
Rebasing is more complex for an arithmetic index. While it works for a Lowe and Dutot index in the exact same way as a geometric index, in general rebasing an arithmetic index changes the weights used to average price relatives because of the way an arithmetic index is factored. The rebased index is still an arithmetic index, but the weights are no longer correct. For example, rebasing a Laspeyres index changes the weights so that they are no longer the base-period expenditure shares—the index is still an arithmetic index (a Lowe index), but products that have seen a larger increase in price since the base period will receive more weight in the index calculation. In practice, however, this theoretical wrinkle is usually ignored, and an arithmetic price index gets rebased by simply dividing the entire index series by the index value in the new base period.